Mathematics is a fascinating subject that plays a vital role in our everyday lives. It helps us solve problems, make decisions, and understand the world around us. To truly excel in math, it is important to develop a strong foundation and adopt the eight mathematical practices. These practices are essential for students to become proficient and confident mathematicians.
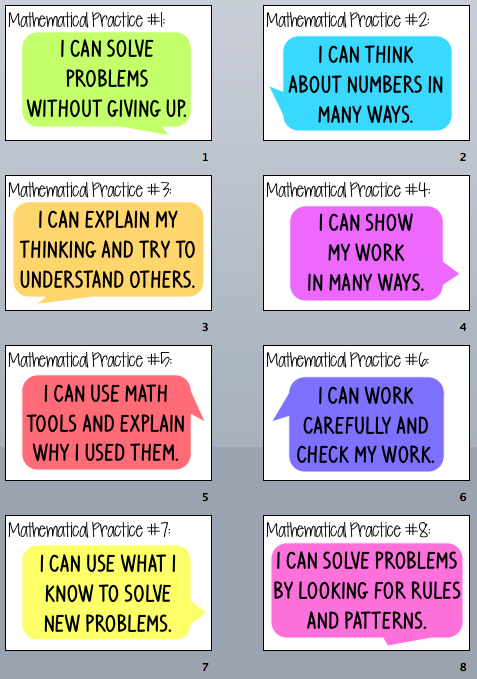
- Make sense of problems and persevere in solving them
The first mathematical practice encourages us to approach problems with a positive mindset and not be deterred by challenges. It emphasizes the importance of understanding the problem before attempting to find a solution. By persevering through difficulties, we develop problem-solving skills that can be applied to various real-life situations.
- Reason abstractly and quantitatively
Mathematics involves abstract thinking and the ability to represent real-world situations using numbers and symbols. This mathematical practice encourages us to think critically, analyze data, and make meaningful connections between mathematical concepts and real-life scenarios.
- Construct viable arguments and critique the reasoning of others
Developing the ability to construct logical arguments and evaluate the reasoning of others is an important aspect of mathematics. This mathematical practice fosters communication and collaboration, as well as the ability to justify mathematical conclusions and identify errors in reasoning.
- Model with mathematics
The fourth mathematical practice highlights the significance of using mathematics as a tool to model and solve real-world problems. It encourages students to represent situations mathematically and use their understanding of mathematical concepts to interpret and analyze the results.
- Use appropriate tools strategically
Technology and other mathematical tools can greatly enhance our understanding and efficiency in solving problems. This mathematical practice emphasizes the importance of selecting and effectively using tools to solve mathematical problems, whether it be calculators, spreadsheets, or graphing software.
- Attend to precision
Precision is key in mathematics. This practice encourages students to communicate precisely and use accurate mathematical language. Attention to detail, including labeling diagrams and using appropriate units, plays a significant role in producing accurate and reliable mathematical results.
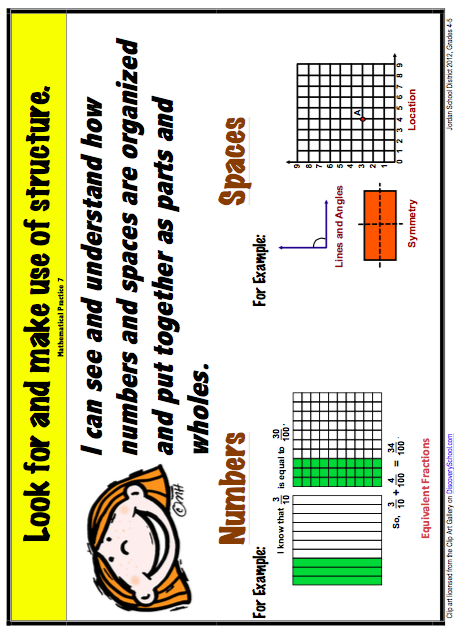
- Look for and make use of structure
The ability to recognize patterns and structures is crucial in understanding and solving mathematical problems. This practice encourages students to examine the underlying structures and relationships of mathematical concepts, enabling them to make connections and apply their knowledge to new situations.
- Look for and express regularity in repeated reasoning
Mathematics often involves repeating patterns and processes. This practice emphasizes the importance of recognizing and generalizing these regularities. By doing so, students can develop efficient and strategic approaches to solving problems, saving time and effort.
By incorporating these eight mathematical practices into our learning, we can develop a deep understanding of mathematics and become confident problem solvers. It is through embracing these practices that we can unlock the full potential of mathematics and its relevance in our lives.
Remember, math is not just about numbers and formulas – it is a powerful tool that empowers us to think critically, solve problems, and make informed decisions. So, let’s embrace the eight mathematical practices and embark on an exciting journey of mathematical exploration!
